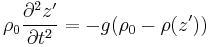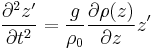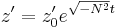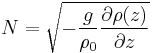Brunt–Väisälä frequency
In atmospheric dynamics, oceanography, and geophysics, the Brunt–Väisälä frequency, or buoyancy frequency, is the frequency at which a vertically displaced parcel will oscillate within a statically stable environment. It is named after David Brunt and Vilho Väisälä.
Contents |
Derivation for a general fluid
Consider a parcel of (water or gas) that has density of 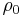 and the environment with a density that is a function of height:
and the environment with a density that is a function of height: 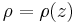 . If the parcel is displaced by a small vertical increment
. If the parcel is displaced by a small vertical increment 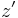 , it will subject to an extra gravitational force against its surroundings of:
, it will subject to an extra gravitational force against its surroundings of:
g is the gravitational acceleration, and is defined to be positive. We make a Newton's method approximation to 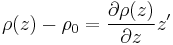 , and move
, and move 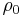 to the RHS:
to the RHS:
The above 2nd order differential equation has straightforward solutions of:
where the Brunt–Väisälä frequency N is:
For negative 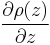 , z' has oscillating solutions (and N gives our frequency). If it is positive, then there is run away growth – i.e. the fluid is statically unstable.
, z' has oscillating solutions (and N gives our frequency). If it is positive, then there is run away growth – i.e. the fluid is statically unstable.
In meteorology and oceanography
In the atmosphere,
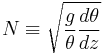 , where
, where  is potential temperature,
is potential temperature,  is the local acceleration of gravity, and
is the local acceleration of gravity, and 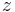 is geometric height.
is geometric height.
In the ocean where salinity is important, or in fresh water lakes near freezing, where density is not a linear function of temperature,
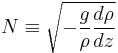 , where
, where  , the potential density, depends on both temperature and salinity.
, the potential density, depends on both temperature and salinity.
Context
The concept derives from Newton's Second Law when applied to a fluid parcel in the presence of a background stratification (in which the density changes in the vertical). The parcel, perturbed vertically from its starting position, experiences a vertical acceleration. If the acceleration is back towards the initial position, the stratification is said to be stable and the parcel oscillates vertically. In this case, N2 > 0 and the frequency of oscillation is given by N. If the acceleration is away from the initial position (N2 < 0), the stratification is unstable. In this case, overturning or convection generally ensues.
The Brunt–Väisälä frequency relates to internal gravity waves and provides a useful description of atmospheric and oceanic stability.